Tag: Temperature

In this post, we will create a circuit to connect a DHT22 temperature and relative humidity sensor to an Arduino Uno and write a class to read the information off the sensor. The sensor signal will be read directly without the use of a ready-made library, allowing the reader to better understand how such code is written. If you are interested in using a ready-made library, you can download one created by Adafruit Industries from the Arduino Libraries or have a look at the actual project on GitHub. The Arduino sketch and code associated with this blog post can be found here on GitHub. The featured image at the beginning of this blog post has been released into the public domain by its author, Fenners and was downloaded from the Wikimedia Commons.

The DHT22 sensor, pictured below, is a small 25mm by 15mm by 8mm white plastic device with slits and holes organized in a grate pattern on its front face allowing for the surrounding air to reach within the sensor. It has four metal leads allowing it to be electrically connected to a circuit. The leads, numbered 1 to 4, from left to right, have the following functionality. Lead 1 is VDD, the power supply, whose voltage must be between 3.3 volts and 5.5 volts. Lead 2 is the data signal lead. We will describe how data is requested and transmitted later on in this post. Lead 3 is unused and should remain unconnected. Finally, lead 4 is ground and must be connected to the power source ground.

Communicating with the DHT22

Communication with the sensor is achieved using the DHT22 data signal lead. The data signal lead is a bidirectional communication signal line. This means that the DHT22 sensor can receive and send information on this line. In it’s idle state, the sensor listens to the signal line waiting for a low, 0 volt, to be applied on the line for at least one millisecond by the Micro Controller Unit (MCU), the Arduino. 20 to 40 microseconds after the low signal reverts to high, the sensor sends a low, 0 volt, for 80 microseconds, then a high, 5 volts, for 80 microseconds to indicate start of transmission. The sensor then sends a series of low and high values, varying in duration, encoding zeroes and ones that will translate into numbers representing the temperature and the relative humidity. The following timing diagram illustrates this sequence.

The sequence of low and high values is similar to the dots and dashes that were discussed in the Morse Code Generator post. For Morse code, the duration of the dot, the short burst, is the unit of time by which all other elements of Morse code are defined. As can be seen in the DHT22 signal timing diagram below, a zero is encoded as a low value lasting 50 microseconds followed by a high value lasting 26 to 28 microseconds and a one is encoded as a low value lasting 50 microseconds followed by a high value lasting 70 microseconds. Thus, the unit of time is determined by how long the low signal lasts. A zero is detected when the low signal is followed by shorter high signal and a one is detected when the low signal is followed by a longer high signal. There are a total of forty of these low and high values forming a sequence of forty zeroes and ones, a sequence of forty bits.

Relative Humidity

The first sixteen bits, or binary digits, represent the relative humidity value in thousandths. The way binary digits work is the same as for decimal digits except that there are only two possible values for each digit, 0 and 1. The minimum relative humidity value is 0, 0.0%, and the maximum relative humidity value is 1000, or 100.0%. The decimal value for the maximum relative humidity value is interpreted thus:

1×10³+0×10²+0×10¹+0×10⁰,
1×1,000 + 0×100 + 0×10 + 0×1.

Each decimal digit represents the value of the digit multiplied by increasing powers of 10, from right to left. The same value represented using binary digits is 1111101000 or

1×2⁹+1×2⁸+1×2⁷+1×2⁶+1×2⁵+0×2⁴+1×2³+0×2²+0×2¹+0×2⁰,
1×512 + 1×256 + 1×128 + 1×64 + 1×32 + 0×16 + 1×8 + 0×4 + 0×2 + 0×1.

Each binary digit represents the value of the digit multiplied by increasing powers of 2, from right to left. Most computers, microprocessors and micro-controllers, the Arduino is no exception, store information in chunks of eight bits, called bytes. As demonstrated above, to represent decimal 1000 in binary requires 10 bits of information. Since this information is stored in 8-bit bytes, 2 bytes of information, or 16 bits, are required to store a value ranging from 0 to 1000. So 1000 stored in binary in chunks of 8-bit bytes is

00000011 11101000

Where the byte on the left is the most significant byte containing the most significant bit also at the left. This is the first bit read from the sensor, and the byte on the right is the least significant byte containing the least significant bit, the last one read, completely at the right. The 16 bits returned by the DHT22 sensor device for a relative humidity of 100% are exactly as depicted, starting at the most significant bit, six zeroes, followed by 5 ones, then one zero, one one, and finally three zeroes.

Temperature

The next 16 bits of the 40 bit sequence contain the temperature. Temperature is in degrees Celsius and span from −40.0 degrees to 80.0 degrees. Temperatures from 0 to 80 degrees are stored the same way as relative humidity values are encoded. 80 degrees is encoded as 800 decimal or 1100100000 in binary which can be stored in 2 bytes as

00000011 00100000

What about negative numbers, values between -40.0 and 0.0 degrees Celsius? In early computers, negative numbers were identified by setting the most significant bit to 1. Hence, five was encoded in binary as 00000101 and minus five as 10000101. This worked, but it was not very convenient as each operation had to check for the value of the most significant bit to decide which operation to perform and because there were two values for zero, a minus zero, 10000000, and a plus zero, 00000000. Another method was devised, the two’s complement method for representing negative numbers. It consists in complementing the binary number, making all zeroes ones and all ones zeroes, and then adding one. For instance, the number five, encoded as 00000101, becomes 11111010 and, if we add one, 11111011. Using the two’s complement negative number representation, negative numbers can be also be identified with their most significant bit, the leftmost bit, set to one.

The interesting thing is this: if you add a number with its two’s complement, the result is zero, exactly what one would expect when adding a number and its negative. The two’s complement of a number that has been two’s complemented is the original number, again, what is expected. Finally, the two’s complement of zero is also zero. These properties of the two’s complement method for representing negative numbers correspond to the mathematical properties of negative numbers, making arithmetic operations straight forward. If Tc(n) is a function returning the two’s complement of a number, we get the following properties for binary operations along with the corresponding properties for arithmetic operations.

So, the DHT22 sensor representation of minus forty is as follows. First, let’s encode forty degrees as 400, ten times forty. The 16-bit binary representation of 400 is 00000001 10010000. To make it negative, we complement the number, making all zeroes ones and all ones zeroes getting 11111110 01101111, and then we add one, getting 11111110 01110000. Temperatures vary in the range from -40.0 degrees Celsius to 80 degrees Celsius which becomes in binary terms:

from 11111110 01110000 to 00000011 00100000.

Checksum

The final 8 bits sent by the DHT22 sensor contain a checksum. Checksums are a method to verify that the data sent is valid by making an arithmetic sum of all values sent and sending a truncated version of the sum last, allowing the receiving device to verify that data was transmitted correctly. The checksum sent by the DHT22 sensor is the sum of the first four 8-bit bytes truncated to the least significant 8 bits. After receiving all 40 bits of data from the sensor, the Arduino program computes the sum of the first four 8-bit bytes, truncates the result to the least significant 8 bits and compares the value to the checksum sent by the sensor. If the values match, the data is deemed valid.

Connecting the DHT22 to an Arduino

The following picture depicts how to connect the different parts using a solderless breadboard, jump wires, and a DHT22 temperature and relative humidity sensor. The sensor’s lead 1, the leftmost one, is connected the 5 volts supply, lead 4, the rightmost one, is connected to the supply’s ground, and lead 2, the signal lead, is connected to digital I/O pin 2.

The Program

The purpose of the program is simple, read temperature and relative humidity from the DHT22 sensor and return the information to the connected computer. The following shows the content of the main sketch which can be found, along with the DHT22 access class, on GitHub.

/*
  DHT22 Temperature / Humidity Serial Decoder Sketch
  Program that requests temperature and humidity from a DHT22 sensor
  and returns the results to the serial port. It is associated with
  the Serial Communication with a Temperature Sensor blog post on
  https://lagacemichel.com
  MIT License
  Copyright (c) 2020, Michel Lagace
*/

#include "DHT22.h"

// DHT serial input/output port
#define DHT22_PORT 2

// Create DHT22 device instance
DHT22 dht(DHT22_PORT);

// Setup the board.
void setup() {
  Serial.begin(9600);
}

// This is the main loop. It requests for a transmission, decodes
// the signal and displays decoded temperature and humidity.
void loop() {
  // Get relative humidity and temperature
  float relativeHumidity = dht.relativeHumidity();
  float temperature = dht.temperature();

  // Send results back to PC
  Serial.print("T: ");
  Serial.print(temperature,1);
  Serial.print("C RH: ");
  Serial.print(relativeHumidity,1);
  Serial.println("%");
  delay(5000);
}

First, the Arduino sketch file starts with a comment stating the purpose of the program, the author and a copyright notice. The program is licensed under the standard MIT license. Next, we include the “DHT22.h” file which declares the DHT22 class. We will cover the content of this file later in this post. Classes and objects were discussed previously in the Programming with Class blog post. We then define the port to use to communicate with the sensor, DHT22_PORT and we instantiate an object of class DHT22, initializing it with the port just specified. The DHT22 object will handle all communications with the external sensor to provide the program with the temperature and relative humidity.

The setup() function sets up the serial communication to communicate with the PC at 9600 baud, or approximately 10 characters per second. In the main loop() function, we get the relative humidity and temperature from the instance of the DHT22 class using the relativeHumidity() and temperature() methods respectively. We then send the information back to the connected computer using the Serial interface’s print() and println() methods. Finally, the program waits five seconds, using the delay() function, before exiting the loop() function which will be repeatedly called forever.

The DHT22.h File

The DHT22.h header file defines the DHT22 class. C++ and .ino files that want to use objects of the DHT22 class must include this file using the ‘#include‘ statement. The header file contains the class definition that declares a destructor and a constructor using the port number to which the DHT22 sensor is connected in its public section. Two accessor methods, temperature()and relativeHumidity() are declared to return the floating point value of the temperature and relative humidity read from the sensor.

Follows a private section declaring the default constructor, the copy constructor and the assignment operator. They are made private to prevent their use. Then we declare three private methods, timeSinceLastRead(), waitForState(), and fetchData(), only accessible from within the class. These methods will be described later in the post. Finally, there is a private section containing the persistent data used within the class. This data includes an integer (int) holding the port number, m_port, used to communicate with the sensor, an array of five bytes (byte) m_data, to contain the forty bits read from the sensor, an unsigned long integer, m_lastRead, containing the last time, in milliseconds since the program started, data was read from the sensor, two floating point numbers (float), m_temperature and m_relativeHumidity, containing the last temperature and relative humidity read from the sensor, and a Boolean flag (bool), m_firstTime, used to indicate if the class instance has been previously used.

/*
  DHT22 Temperature / Humidity Controller Class Header
  DHT22 temperature and relative humidity sensor handling class. This class
  allows the instanciation of objects that communicate with a DHT22 sensor
  connected to a digital input/output port on an Arduino micro-controller.
  This code is associated with the Serial Communication with a Temperature
  Sensor blog post on https://lagacemichel.com
  MIT License
  Copyright (c) 2020, Michel Lagace
*/

#if !defined(DHT22_H)
#define DHT22_H

#include "Arduino.h"

class DHT22 {
  public:
    // Orthodox cannonical form
    ~DHT22(); // Destructor

    // Constructor connecting digital I/O port to DHT22 device
    DHT22(int port); // Constructor

    // Get temperature and relative humidity
    float temperature();
    float relativeHumidity();

  private:
    // Unusable and hidden orthodox cannonical form
    DHT22();  // Default constructor
    DHT22(const DHT22&); // Copy constructor
    DHT22& operator = (const DHT22&); // Assignment operator

    // Internal methods
    unsigned long timeSinceLastRead() const;
    int waitForState(bool state) const;
    void fetchData();
    

  private:
    int m_port;               // I/O pin connected to sensor
    byte m_data[5];           // Data read from DHT22 sensor
    unsigned long m_lastRead; // Last time data was read in milliseconds since program start
    float m_temperature;      // Temperature in degrees Celsius
    float m_relativeHumidity; // Relative humidity in %
    bool m_firstTime;         // Flag if first time around
};
#endif

The DHT22.cpp File

The “DHT22.cpp” file contains the implementation of the DHT22 class methods. It starts with the standard header with title, description, license and copyright notice in a comment. It then includes the class definition from header file “DHT22.h” and defines a few timing values that will be used throughout the code. The CYCLES_PER_COUNT definition is the number of CPU cycles that the waitForState() method uses on average every time it checks if the signal from the DHT22 sensor has achieved the desired level, HIGH or LOW. This value was measured as part of a separate benchmark program. The TIMEOUT_MICROSECONDS value is the maximum time, in microseconds, to wait for the desired level. The TIMEOUT value corresponds to the number of times the signal level needs to be checked to reach a timeout. The TIMEOUT value is defined using the F_CPU definition found in the “Arduino.h” header file. F_CPU defines the CPU frequency in cycles per second for the Micro Controller used. For the Arduino Uno, this value is 16,000,000. The last three definitions specify in milliseconds delay values of ONE_SECOND, TWO_SECONDS, and TWO_MILLISECONDS.

/*
  DHT22 Temperature / Humidity Controller Class Body
  DHT22 temperature and relative humidity sensor handling class. This class
  allows the instanciation of objects that communicate with a DHT22 sensor
  connected to a digital input/output port on an Arduino micro-controller.
  This code is associated with the Serial Communication with a Temperature
  Sensor blog post on https://lagacemichel.com
  MIT License
  Copyright (c) 2020, Michel Lagace
*/

#include "DHT22.h"

#define CYCLES_PER_COUNT 50
#define TIMEOUT_MICROSECONDS 300
#define TIMEOUT TIMEOUT_MICROSECONDS/CYCLES_PER_COUNT*F_CPU/1000000
#define ONE_SECOND 1000
#define TWO_SECONDS 2000
#define TWO_MILLISECONDS 2

DHT22 Class Constructor and Destructor

The class constructor initializes the DHT22 sensor port value, m_port, to the value passed as a parameter to the constructor. All data values in the m_data array are initialized to 0, the last time in milliseconds since the program started that the sensor was read, m_lastRead, is also initialized to 0. The first time through flag, m_firstTime, is set to true, and both floating point values for the temperature and relative humidity, m_temperature and m_relativeHumidity, are initialized to 0.0. The DH22 class destructor does not perform any action.

// DH22 constructor, accepts Arduino digital I/O port number
DHT22::DHT22(int port) {
  m_port = port;
  m_data[0] = 0;
  m_data[1] = 0;
  m_data[2] = 0;
  m_data[3] = 0;
  m_data[4] = 0;
  m_lastRead = 0;
  m_firstTime = true;
  m_temperature = 0.0;
  m_relativeHumidity = 0.0;
}

// DH22 destructor
DHT22::~DHT22() {
}

DHT22 Class Accessors

Accessors are the class methods used to access the DHT22 sensor temperature and relative humidity. Both methods call the fetchData() method to read information, if required, from the DHT22 sensor, then return the sought information. The temperature() method returns a floating point value representing the temperature in degrees Celsius and the relativeHumidity() method returns a floating point value representing the relative humidity as a percentage.

// Return temperature
float DHT22::temperature() {
  // Get data from sensor and return temperature read
  fetchData();
  return m_temperature;
}

// Return relative humidity
float DHT22::relativeHumidity() {
  // Get data from sensor and return relative humidity read
  fetchData();
  return m_relativeHumidity;
}

DHT22 Class timeSinceLastRead( ) Method

The timeSinceLastRead() method returns an unsigned long integer containing the time in milliseconds since the fetchData() method actually read data from the DHT22 sensor device. The fetchData() method stores the number of milliseconds since the program was started in variable m_lastRead every time it reads data from the sensor and it calls the timeSinceLastRead() method before attempting to read data from the sensor, ensuring that at least two seconds have elapsed since the last sensor device request.

The timeSinceLastRead() method first gets the current number of milliseconds since program start using the millis() function. It then checks if the value has overflowed, that is if the unsigned long value went further than the maximum value an unsigned long can hold. This value is actually 4,294,967,295, corresponding to approximately 49.7 days. After an overflow, the number of milliseconds since the program started restarts at zero. If an overflow occurs, time is computed by adding the two’s complement of the last time read corresponding to the time left to reach the overflow added to the number of milliseconds after the overflow, providing the actual number of milliseconds since the time was stored in m_lastRead. Two’s complement is computed by complementing the value, turning all ones into zeroes and all zeroes into ones using the unary bitwise not operator, ‘~‘, and then adding one. Otherwise, the method simply computes the difference between the current time and the last time m_lastRead was updated.

// Return the number of milliseconds since last time read
unsigned long DHT22::timeSinceLastRead() const {
  // Get current processor time
  unsigned long currentMilliseconds = millis();
  unsigned long timeSince = 0;

  // Check if time wrapped around, if so use two's complement
  if (currentMilliseconds < m_lastRead) {
    timeSince = ~m_lastRead + 1 + currentMilliseconds;
  }

  // Otherwise use difference
  else {
    timeSince = currentMilliseconds - m_lastRead;
  }

  // Return elapsed time
  return timeSince;
}

DHT22 Class waitForState( ) Method

The waitForState() method repeatedly checks if the DHT22 sensor data lead has reached the desired state, HIGH or LOW, as specified in the method’s parameter, state, or if a timeout has been reached. The method returns the number of times the sensor line has been checked, or 0 if a timeout occurred.

// Wait for serial line to reach a state and return relative time
int DHT22::waitForState(bool state) const {
  int count = 0;
  while ((bool)digitalRead(m_port) != state) {
    count++;
    if (count >= TIMEOUT) {
      count = 0;
      break;
    }
  }
  return count;
}

DFT22 Class fetchData( ) Method

The fetchData() method is the actual method that reads data from the DHT22 sensor, through the waitForState() method, and that computes the temperature and relative humidity. First, the method checks if this the first time the method is being called or if more than two seconds have elapsed since the last time sensor data has been read. If not, then the method does nothing and returns. If it is the first time the method is called, the DHT22 sensor port is put in input mode with a pull-up resistor for one second. Then, the port is put in OUTPUT mode, a LOW signal is sent for two milliseconds, then the port is put back in INPUT_PULLUP mode, providing a HIGH signal at the port, thus completing the request for data signal.

Next, we enter the time critical section of the code where we will be measuring the timing of the signal sent back by the DHT22 sensor. For the whole period of a maximum of approximately 3 milliseconds, we disable interrupts, allowing us to precisely compute time. Because the Arduino’s time computing functions require interrupts to be enabled, we use the number of CPU cycles spent detecting a change of state, between HIGH or LOW, within the waitForState() method. Interrupts are disabled using the noInterrupts() Arduino built-in function and re-enabled using the interrupts() Arduino built-in function.

While interrupts are disabled, the code first checks for the signal to go from HIGH to LOW, then from LOW to HIGH, and back to LOW again. This corresponds to the start of transmission signal from the DHT22 sensor. The low and high signals last 80 microseconds each but there is no need to check the timing except for timeouts. This is why we check for a positive integer everytime waitForState() is called in order to continue processing. After sending the start of of transmission, the DHT22 sensor proceeds with the forty bits of data. For each bit, the counter values for the signal to go from LOW to HIGH and then from HIGH to LOW are gathered from appropriate calls to the waitForState() method. If there are no timeouts, the bit value is stored in the appropriate byte as explained after the code listing below.

// Fetch data from sensor
void DHT22::fetchData() {
  // We will access sensor on the very first time and if more than two
  // seconds have passed since last access.
  if (m_firstTime || (timeSinceLastRead() > TWO_SECONDS)) {

    // First time around, wait at least one second for sensor to settle
    if (m_firstTime) {
      m_firstTime = false;
      pinMode(m_port, INPUT_PULLUP);
      delay(ONE_SECOND);
    }

    // Send request signal to reMad temperature and relative humidity from device.
    pinMode(m_port, OUTPUT);
    digitalWrite(m_port, LOW);
    delay(TWO_MILLISECONDS);
    pinMode(m_port, INPUT_PULLUP);

    // Since timings are critical, prevent interrupts while DHT22 transmits
    noInterrupts();

    // Get Start of Transmission, falling, rising, then falling edges
    // Interval: 80 micro-seconds, no need to check
    int lowCounter = 0;
    int highCounter = 0;
    highCounter = waitForState(LOW);
    if (highCounter > 0) {
      lowCounter = waitForState(HIGH);
      if (lowCounter > 0) {
        highCounter = waitForState(LOW);
      }
    }

    // Get 40 bits of data and store them in the data array
    if (highCounter > 0) {
      for (int bitN = 0; bitN < 40; bitN++) {     // 40 bits, 5 x 8-bit bytes
        lowCounter = waitForState(HIGH);          // Byte 0: Relative Humidity MSB
        if (lowCounter > 0) {                     // Byte 1: Relative Humidity LSB
          highCounter = waitForState(LOW);        // Byte 2: Temperature MSB
          if (highCounter > 0) {                  // Byte 3: Temperature LSB
            int byteN = bitN/8;                   // Byte 4: Checksum
            m_data[byteN] <<= 1;
            if (highCounter > lowCounter) {       // Low 50us, High 25us -> 0
              m_data[byteN] |= 1;                 // Low 50us, High 70us -> 1
            }
          }
        }
      }
    }
    // Reception complete, interrupts are re-enabled
    interrupts();

    // Save the time of last data transfer
    m_lastRead = millis();

    // Compute temperature and relative humidity if data is valid
    byte checksum = m_data[0] + m_data[1] + m_data[2] + m_data[3];
    if (m_data[4] == checksum) {
      m_relativeHumidity = int((m_data[0] << 8) + m_data[1])/10.0;
      m_temperature = int((m_data[2] << 8) + m_data[3])/10.0;
    }
    else {
      m_relativeHumidity = 0.0;
      m_temperature = 0.0;
    }
  }
}

In the middle of the loop that gathers the 40 bits above, we get the number of counts for which the signal is LOW and the number of counts for which the signal is HIGH in the lowCounter and highCounter variables respectively. As explained previously, the corresponding bit is ‘0‘ if highCounter is smaller than lowCounter and ‘1‘ if highCounter is greater than lowCounter. Each sequence of 8 bits is stored in its own byte in the m_data array, first bit read in the byte’s most significant bit. Bits 0 to 7 are stored in m_data[0], bits 8 to 15 in m_data[1], and so on. We determine in which m_data array element to store a bit by dividing the bit number, bitN, by 8 since there are 8 bits in each byte. Once we know which m_data array element to store the bit in, we do two operations. First we push the bits already in the array element by one bit to the left using the shift left operator (‘<<=‘). This is equivalent to multiplying the data by 2, pushing all bits to the left and setting the least significant bit to 0. If highCounter is larger than lowCounter, we then set the least significant bit of the array element to 1 using the ‘or’ binary operator, ‘|=‘. The ‘or’ operator takes each bit in the array element and performs an ‘or’ operation with each bit of the operand, in this case 1, or 00000001 in binary. If both bit values are ‘0‘ then the result is ‘0‘. If any of the bit values are ‘1‘ then the resulting bit is ‘1‘. At the end of the loop, all 40 bits are stored in the m_data array.

As soon as interrupts are re-enabled, we store the current time in m_lastRead, which will prevent the sensor from being read for the next two seconds. Finally, we compute the checksum of the first four bytes received from the sensor and compare it to the 5th byte received, the sensor checksum. If checksums match, we compute the temperature and relative humidity by creating a 16 bit unsigned value, shifting the most significant byte 8 bits to the left and adding the least significant byte. We then convert the number to a signed integer, and divide the signed number by 10.0, automatically converting the result to a floating point value. The temperature and relative humidity values are saved in the m_temperature and m_relativeHumidity variables respectively for future use. If there was a checksum error, both temperature and relative humidity values are set to 0.0.

Putting It to Work

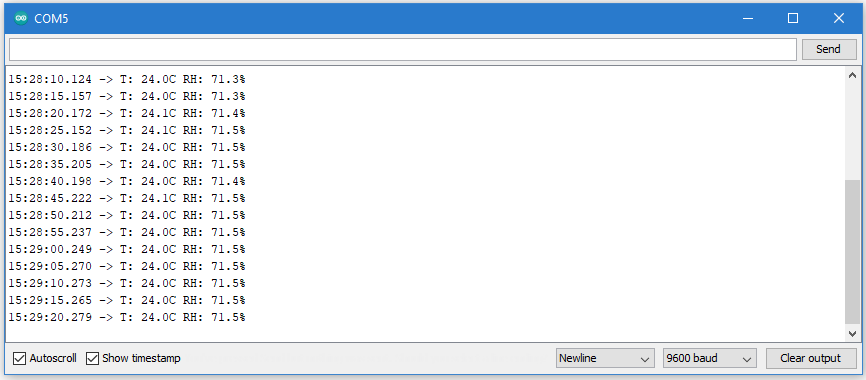
Build the circuit shown above and connect the Arduino Uno to your computer using a USB cable. On the computer, within the Arduino IDE, compile and download the sketch then press the control, shift, and M keys simultaneously. This will make the Serial Monitor window appear. Every five seconds, the Arduino program will send the current temperature and humidity as a character string back to the computer. The text is displayed on the Serial Monitor window and the output should look like the following: